Deux jours de formation, suite et fin

Le prix de l’option est donné par l’espérance sous probabilité risque neutre du payoff terminal actualisé $C = E[Payoff \times e^{-rT}]$ , soit la formule de Black-Scholes :

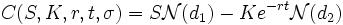
$C(S,K,r,t,\sigma) = S \mathcal{N}(d_1) - K e^{-rt}\mathcal{N}(d_2)$

De même,le prix théorique d’une option de vente (put), de payoff $( K - \mathcal{S}_{T} )^{+}=\max(K-S_{T} ; 0)$ est donné par :

$P(S,K,r,t,\sigma) = -S \mathcal{N}(-d_1) + K e^{-rt}\mathcal{N}(-d_2)$

avec

$\mathcal{N}$ la fonction de répartition de la loi normale centrée réduite $\mathcal{N}\left( 0,1 \right)$ , c’est-à-dire $\mathcal{N}(x) = \int_{-\infty}^{x} \frac{1}{\sqrt{2\Pi}}e^{-\frac{1}{2}u^2} du$
$d_1 = \frac{1}{\sigma\sqrt{t}} \left[ \ln \left( \frac{S}{K} \right) + \left( r + \frac{1}{2}\sigma^2 \right)t \right]$
$d_2 = d_1 - \sigma \sqrt{t}$

Laisser un commentaire Annuler la réponse

Articles similaires